A Geometria do Futebol: um Facilitador no Ensino Aprendizagem

A Geometria do futebol: Um facilitador no ensino aprendizagem

O objetivo desta monografia foi trabalhar os conceitos geométricos no futebol. Mostrar que a Matemática, em particular, a Geometria, pode ser uma ferramenta para interpretar uma partida de futebol e suas características, ou seja, mostrar que a Geometria é o ponto de encontro entre a Matemática como teoria e a Matemática como um recurso. Através de uma análise detalhada de vários autores, mostraremos que a Matemática, em especial a Geometria é uma ciência muito interessante, muito importante no nosso dia-a-dia e muito instigante. Porém nossa sociedade coloca a Matemática como uma disciplina complicada, difícil e aterrorizante. Através da Educação Matemática podemos demonstrar o contrário, podemos mostrar como a Matemática, a Geometria é fascinante, gostosa e útil. Sendo a Geometria um ponto de encontro entre a Matemática como teoria e a Matemática como um recurso, ela é um caminho para desenvolver o pensamento e a compreensão para alcançar o nível mais alto de uma teoria formal. Já que a Geometria é o ponto de encontro entre a Matemática como teoria e a Matemática como um recurso, temos que usar nossa imaginação e mostrar como a Geometria está presente no nosso dia-a-dia, em todos os lugares: principalmente nos campos de futebol, nas quadras de esporte, na arquitetura, na engenharia, nas embalagens dos produtos, no artesanato e na tecelagem, por isso a Geometria é descrita como um corpo de conhecimento fundamental para a compreensão do mundo e participação ativa do homem na sociedade, pois facilita a resolução de problemas de diversas áreas do conhecimento e desenvolve o raciocínio visual.

Palavras-chaves: Futebol; Geometria; Esquemas táticos; Aplicações.

INTRODUÇÃO

Trata-se no presente trabalho dos conceitos geométricos, em especial os conceitos da Geometria Plana aplicados ao futebol de um modo geral. Mostra a Geometria de outra maneira, ou seja, uma Geometria aplicada a um esporte que é a paixão nacional. Vamos trabalhar Geometria falando a linguagem do aluno e abordando assuntos discutidos a todo instante. Associamos um esporte popular, de massa, a uma disciplina que é considerada difícil, chata, aterrorizante, que poucos gostam, ou seja, a Matemática.
Quem nunca ouviu falar do quadrado mágico que foi rotulado pelos jornalistas e treinadores de todo o mundo com referência a qualidade dos jogadores brasileiros na Copa do Mundo de Futebol realizada na Alemanha em 2006. As triangulações sempre citadas nos comentários de qualquer partida de futebol. Os esquemas táticos: 4-4-2, 3-5-2, 4-3-3, alguém já analisou o desenho geométrico, ou seja, as figuras que esses esquemas formam?

O objetivo desta monografia foi trabalhar os conceitos geométricos no futebol. Mostrar que a Matemática, em particular, a Geometria, pode ser uma ferramenta para interpretar uma partida de futebol e suas características, ou seja, mostrar que a Geometria é o ponto de encontro entre a Matemática como teoria e a Matemática como um recurso.

Inicialmente esclareceremos como é a Educação Matemática que temos que abordar nos dias atuais. Após, serão tratados alguns conceitos matemáticos, em especial alguns tópicos de Geometria Plana. Por fim abordaremos a parte aplicada ao futebol, desde a bola de futebol, o campo de jogo, suas medidas, algumas curiosidades e as diferentes variações táticas de diversos times de futebol.

Deste modo o presente trabalho será de grande valia, pois pode - se trabalhar de uma forma diferente um assunto que é visto por todos como de difícil entendimento. Ensinar com criatividade, baseando-se no dia - a - dia do aluno, mostrando que a Matemática especificamente a Geometria, não são apenas fórmulas e cálculos.

Educação Matemática

A Educação Matemática não pode ser aquela baseada apenas nas teorias dos livros, das apostilas ou do quadro negro. Hoje o contexto atual exige uma educação muito mais complexa, completa, ou seja, uma educação que atinja o mundo de uma forma global.

...chama-se a atenção para a necessidade de se relacionar a matemática com os demais setores da sociedade, sobretudo reconhecendo os novos desenvolvimentos das ciências e da tecnologia. O grande desafio que nós, educadores matemáticos encontramos é tornar a matemática interessante, isto é, atrativa, relevante, isto é útil; e atual, isto é, integrada no mundo de hoje (D?AMBRÓSIO, 2001, p. 14 - 15).

Assim é na Educação Matemática que encontramos o apoio necessário para tal transformação.

A educação matemática que queremos é aquela que se estenda muito além dos muros da escola do Ensino Fundamental, do Ensino Médio e do Ensino Superior, que forme educadores e pesquisadores em Ensino de Matemática comprometidos com o ensino formal e não formal (FAINGUELERNT, 2004, p. 07 ).

Diante disto a importância da Educação Matemática se mostra presente. O próprio cotidiano do aluno exige do professor tal tipo de adaptação. Atualmente o que importa é tornar o ensino prazeroso, interessante, criativo e o mais próximo possível da realidade do aluno.

Não há dúvida que numa atividade cujo objetivo é a formação do indivíduo, como é o caso do ensino, não se pode abrir mão do acesso ao conhecimento científico. Mas, levar em consideração as diversas visões deste conhecimento, introduz uma nova concepção de formação, uma formação cuja referência é ao mesmo tempo a ciência e o senso comum. ( MAIA, 2000a, p.25 ).

É importante considerar também que não se deve apenas valorizar o conhecimento científico em detrimento do conhecimento popular, ou seja, o conhecimento científico é muito importante, mas não se pode ignorar o conhecimento popular do aluno, ou seja, falar a linguagem do aluno, aproximar ao máximo da realidade dele.

A Dificuldade de aprendizagem da Geometria

Matemática, Geometria, fórmulas, números, letras, figuras, áreas, volumes, medidas, etc, normalmente são encaradas pelos educandos como um verdadeiro castigo, uma disciplina aterrorizante, que é imposta aos alunos, com muita teoria, muitas fórmulas e pouca prática. Com isso os alunos já chegam traumatizados, com medo, detestando sem nem mesmo conhecer. Já chegam com uma barreira, um obstáculo, sem saber o que é.

O papel do educador é fazer com que esse mito de ser uma disciplina difícil, complicada, com muitas fórmulas apenas e desinteressante, não condiz com a realidade. Temos que mostrar o lado bom da Matemática, da Geometria, as aplicações, instigar o aluno a usar a Matemática para facilitar sua vida no cotidiano. Para isso é preciso inovar, criar, usar e abusar da criatividade para que possamos fazer com que o aluno se interesse por essa disciplina empolgante.

As apostilas, os livros, ou seja, o material didático também contribui significativamente para um ensino deficiente, faltam mostrar as aplicações, com isso tornando o ensino prazeroso e interessante aos alunos.

...alguns livros didáticos também contribuem para a origem de vários problemas, pois as situações de ensino apresentadas naqueles que analisamos e que são propostas para os alunos, de maneira geral, pela maioria dos professores, não enfatizam suficientemente a coordenação de registros de representação semiótica e a importância da figura para a visualização e exploração. Os problemas geométricos propostos por esses livros privilegiam resoluções algébricas, e poucos exigem raciocínio dedutivo ou demonstração. E ainda, quase não existe a passagem da geometria empírica para a geometria dedutiva, além de poucos trabalhos focarem a leitura e a interpretação de textos matemáticos. Essas abordagens criam no aluno concepções inadequadas no que diz respeito ao aprimoramento dos conceitos geométricos, (MANRIQUE, 2004).

De acordo com Pavanello citado por Nascimento ( SBEM, 2004 ):
Além de uma deficiência dos livros didáticos, outro fator importante é o tempo, ou seja, em algumas escolas o conteúdo geométrico é tratado apenas no final do livro didático e muitas vezes não dá tempo para ver o conteúdo, e quando sobra tempo, o mesmo não é visto completo e tem ficado relegado a um plano secundário.

Não podemos deixar de citar também que o desinteresse sobre a Matemática e a Geometria vem da falta de significados para o conteúdo que está sendo ensinado. Está faltando mostrar para que o aluno está estudando esse conteúdo, o que ele vai fazer com isso, onde irá aplicá-lo. Porque em muitos casos os alunos não têm dificuldades, mas sim um desinteresse, porque não consegue ligar a matéria ensinada a sua vida, ao seu mundo, não consegue usar a Matemática como uma ferramenta facilitadora e sim pensam na Matemática como um obstáculo.

A Geometria Aplicada: uma necessidade atual

A Geometria está sempre presente em nossas vidas, é só olharmos nosso cotidiano, sempre tem uma figura geométrica, um ângulo, uma área, um volume para ser calculado, uma medida para ser transformada, um espaço para ser inovado, e isso é possível com a ajuda da Geometria.

Sobre a importância da Geometria, Lorenzato ( 1995 ) diz que esta tem função essencial na formação dos indivíduos, pois possibilita uma interpretação mais completa do mundo, uma comunicação mais abrangente de idéias e uma visão mais equilibrada da Matemática.

Conforme ( MAIA (b), 2000, p. 25 ), dizia: A busca da funcionalidade da Matemática é então uma das características da representação do professor, ou seja, dar uma função para o conteúdo que está sendo ensinado. Já Hershkowitz citado por Fainguelernt ( 1999, p. 51 ), dizia:

Sendo a Geometria um ponto de encontro entre a Matemática como teoria e a Matemática como um recurso, ela é um caminho para desenvolver o pensamento e a compreensão para alcançar o nível mais alto de uma teoria formal. Somente quando essa perspectiva é atingida, a noção de estrutura matemática faz sentido.

A Matemática só consegue alcançar o seu significado, o seu objetivo, quando conseguimos pegar sua teoria e transformá-la em um recurso, numa ferramenta para desenvolvimento social e pessoal, ou seja, a Geometria é um instrumento, um facilitador para que possamos entender alguns acontecimentos cotidianos.

Para tornar o ensino mais aplicado, mais acessível para o aluno, de forma que ele consiga usar a Matemática como uma ferramenta que irá ajudá-lo na sua caminhada, a linguagem desempenha um papel importante na constituição deste conhecimento. Freitas citado por Zuchi ( 2004, p. 49 ), dizia:

Ao mesmo tempo em que a linguagem é um fator importante para o desenvolvimento mental da criança, exercendo uma função organizadora e planejadora do seu pensamento, ela tem também uma função social e comunicativa. Por meio da linguagem a criança é exposta ao conhecimento humano e adquire conceitos sobre o mundo que a rodeia, apropriando-se da experiência acumulada pelo gênero humano no discurso da história social.

A linguagem do professor é importantíssima para a compreensão e desenvolvimento do aluno. Muitas vezes o aluno não consegue ter uma compreensão com o professor, por causa de uma linguagem muito científica, muito formal, mas ao pedir um auxílio ao colega de classe, este falando a linguagem simples, informal, consegue passar de forma clara e tirar a dúvida do mesmo. Na maioria dos casos é necessário que o professor atinja seus objetivos usando uma linguagem adequada ao aluno.

Tópicos elementares de Geometria

A geometria no Ensino Fundamental

A Geometria é construída a partir de três idéias: a idéia de ponto, de reta e de plano, ou seja, os conceitos primitivos. Os matemáticos aceitam essas idéias sem tentar explicá-las.

Segundo Bongiovanni et. al. ( 2002 ), podemos ter idéia de ponto observando marcas de lápis feitas no papel, estrelas no céu, grãos de areia, marca do penalty no campo de futebol, etc. Os pontos são indicados por letras maiúsculas.

Figura 1: Representação de ponto

Temos idéia de reta se imaginarmos um fio, sem começo nem fim, bem esticado. Uma reta é um conjunto de pontos infinitos, e é sempre representada por uma letra minúscula.

Figura 2: Representação de reta

Já quando existe um ponto de origem, pertencente a reta, ou seja, sabe-se onde começa a reta, mas não sabemos o fim, chamamos de semi-reta.

Figura 3: Representação de semi-reta

Agora, se considerarmos apenas um pedaço dessa reta, com origem e fim, teremos a idéia de segmento, ou seja, segmento de reta AB.

Figura 4: Representação de segmento de reta

Outro conceito primitivo é o plano, ou seja, se imaginarmos que é possível prolongar o tampo de uma mesa em todas as direções, teremos a idéia de plano. O campo de futebol é um plano, o chão da sala, sempre imaginando que sempre prolonga, não tem fim. Para traçar um plano é necessário pelo menos três pontos não alinhados. Podemos concluir também que dado um plano ?, nele existem infinitos pontos e infinitas retas pertencentes a este plano.

Figura 5: Representação de plano

Depois de conhecermos os conceitos primitivos, de ponto, de reta e de plano, já podemos entender os conceitos de figura geométrica.

Figura geométrica é qualquer conjunto de pontos. Uma figura geométrica é plana se todos os seus pontos pertencem a um mesmo plano.

Um exemplo de figuras geométricas são os polígonos. Quando o contorno de uma curva fechada simples é constituído apenas de segmentos de retas consecutivos e não colineares, dizemos que a figura geométrica é um polígono.

Os polígonos podem ser classificados de acordo com o número de lados ou ângulos.

Tabela 1: Classificação dos polígonos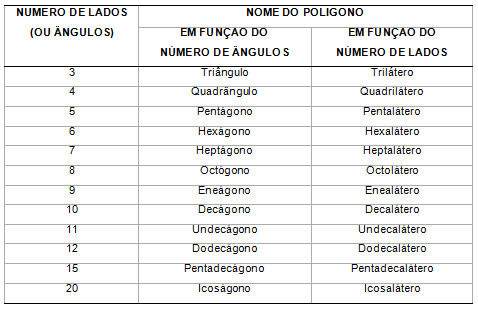

Fonte: SOMATEMÁTICA (2008)

Os polígonos mais comuns e que iremos explorar nesta pesquisa são os triângulos e os quadriláteros notáveis.

Segundo Dolce et al. (1993), os triângulos são classificados de acordo com os seus lados e de acordo com seus ângulos:

• Triângulo equilátero: se, e somente se, têm os três lados congruentes.

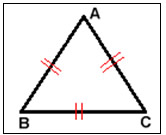
Figura 6: Triângulo equilátero

• Triângulo isósceles: se, e somente se, têm os dois lados congruentes.

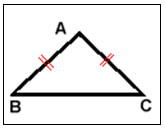
Figura 7: Triângulo isósceles

• Triângulo escaleno: se, e somente se, dois quaisquer lados não são congruentes

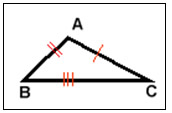
Figura 8: Triângulo escaleno

• Triângulo acutângulo: triângulo que possui todos os ângulos agudos, ou seja, todos os seus ângulos são menores que 90 graus.

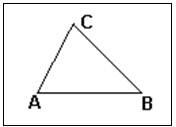
Figura 9: Triângulo acutângulo

• Triângulo retângulo: triângulo que possui um ângulo reto, ou seja, um de seus ângulos mede 90 graus.

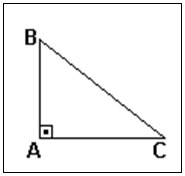
Figura 10: Triângulo retângulo

• Triângulo obtusângulo: triângulo que possui um ângulo obtuso, ou seja, um de seus ângulos tem medida maior que 90 graus.

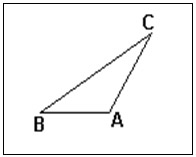
Figura 11: Triângulo obtusângulo

Já os quadriláteros são polígonos simples de quatro lados. Os quadriláteros notáveis são os trapézios, os paralelogramos, os retângulos, os losangos e os quadrados.

Trapézio é um quadrilátero plano convexo se, e somente se, possui dois lados paralelos. Esses lados paralelos são as bases do trapézio. Se analisarmos os outros dois lados que não são as bases podemos classificar o trapézio em:

• Trapézio isósceles: se os outros dois lados forem congruentes.

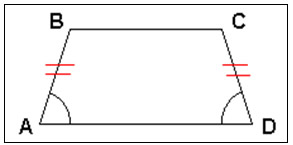
Figura 12: Trapézio isósceles

• Trapézio escaleno: se os outros dois lados não forem congruentes.

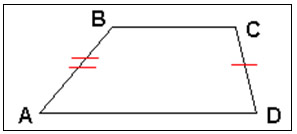
Figura 13: Trapézio escaleno

• Trapézio retângulo ou bi-retângulo: quando tem dois ângulos retos.

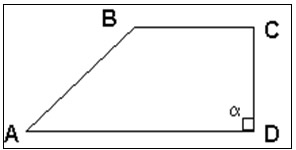
Figura 14: Trapézio Retângulo

O paralelogramo é um quadrilátero plano convexo se, e somente se, possui os lados opostos paralelos.

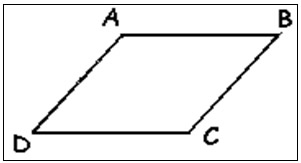
Figura 15: Paralelogramo

O retângulo é um quadrilátero plano convexo se, e somente se, possui os quatro ângulos congruentes.

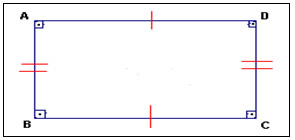
Figura 16: Retângulo

O losango é um quadrilátero plano convexo se, e somente se, possui os quatro lados congruentes.

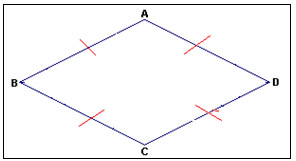
Figura 17: Losango

O quadrado é um quadrilátero plano convexo se, e somente se, possui os quatro ângulos congruentes e os quatro lados congruentes.

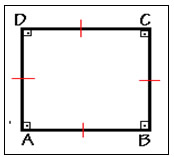
Figura 18: Quadrado

Geometria X Futebol

Diante da necessidade de levar o conhecimento adquirido em sala de aula e aplicá-lo ao nosso dia-a-dia, temos que abusar da criatividade, inventar e falar a linguagem que o aluno consiga entender de forma fácil, prazerosa e interessante.

A Geometria é descrita como um corpo de conhecimentos fundamental para a compreensão do mundo e participação ativa do homem na sociedade, pois facilita a resolução de problemas de diversas áreas do conhecimento e desenvolve o raciocínio visual. Está presente no dia-a-dia como nas embalagens dos produtos, na arquitetura das casas e edifícios, na planta de terrenos, no artesanato e na tecelagem, nos campos de futebol e quadras de esporte, nas coreografias das danças e até na grafia das letras. Em inúmeras ocasiões, precisamos observar o espaço tridimensional como, por exemplo, na localização e na trajetória de objetos e na melhor ocupação de espaços ( FILLOS, 2006 ).

Geometria x Bola de Futebol

Se refletirmos um pouco sobre o principal instrumento para a realização de um jogo de futebol, ou seja, a bola, podemos observar que sua confecção é realizada através de várias figuras geométricas.

Segundo Morelli citado por Corrêa ( 2001, p. 35 ):

Antes, a vaquinha é que ia para o sacrifício. O couro de cada animal rendia seis bolas. Hoje as fábricas usam tiras de poliuretano, um tipo de plástico derivado do petróleo. O poliuretano é mais elástico do que o couro, tem espessura constante e não encharca tanto. Uma prensa especial corta o plástico em gomos de seis e cinco lados. Pegue uma bola e conte. São sempre trinta e dois pedaços ( vinte hexágonos e doze pentágonos ).

Figura 19: Bola de futebol de campo

"A esta figura formada de 12 faces pentagonais e 20 faces hexagonais chama-se icosaedro truncado. O icosaedro truncado é um dos treze poliedros conhecidos como sólidos de Arquimedes" ( FURUYA, 2002 ).

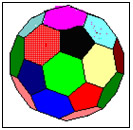
Figura 20: Icosaedro truncado

Os Sólidos de Arquimedes ou poliedros semi-regulares são poliedros convexos cujas faces são polígonos regulares de mais de um tipo. Todos os seus vértices são congruentes, isto é, existe o mesmo arranjo de polígonos em torno de cada vértice. Além disso, todo vértice pode ser transformado em outro vértice por uma simetria do poliedro ( WIKIPEDIA, 2007 ).

O Campo de futebol

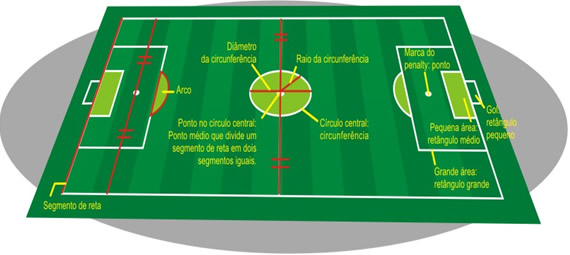
Se observamos o campo de futebol podemos identificar nele várias figuras geométricas, vários ângulos, segmentos de retas, pontos, circunferências, raio, diâmetro, perímetro, áreas, diagonais, arco, podemos trabalhar com medidas e suas transformações, ou seja, metros e centímetros.

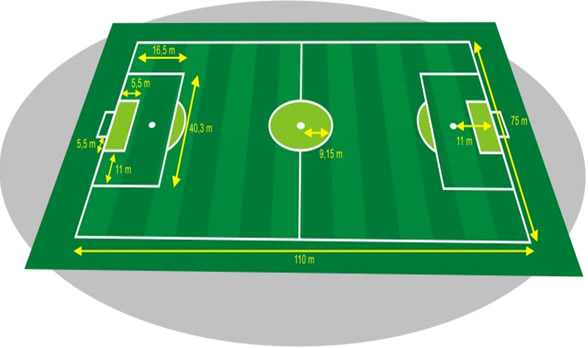
Você já calculou o perímetro de um campo de futebol, suas áreas, área do gol, a área do círculo central, seu diâmetro, a diagonal do campo, são alguns tópicos que iremos mostrar baseado na figura 21 e 22:

Figura 21: O campo e suas medidas oficiais

Segundo Silva ( 2004 ):

Um campo de futebol tem 110 m de comprimento e 75 m de largura, qual o seu perímetro, ou seja, a medida do contorno do campo?

Perímetro = 2 x ( b + h ) , onde, b = comprimento e h = largura
P = 110 m + 110 m + 75 m + 75 m = 2 x ( 110 m + 75 m )
P = 2 x ( 185 m )
P = 370 m
O perímetro é de 370 m.

Já sabemos que as dimensões do campo de futebol são 110 m x 75 m, vamos calcular agora sua área:

Área = Base x Altura ( A = b.h ), onde, b = comprimento e h = largura
Medidas do campo = 110 m x 75 m
A_{do campo} = 110 m x 75 m
A_{do campo} = 8.250 m²
O campo de futebol possui 8.250 m².

Sabendo que a área total do campo é 8.250 m², e nessa área estão 22 jogadores, vamos calcular a área equivalente a cada um desses 22 jogadores.

Campo = 8.250 m²
Números de jogadores = 22
A_{de cada jogador} = 8.250 m² / 22 (área total de 8.250 m² dividida por 22 jogadores)
A_{de cada jogador} = 375 m²
Cada jogador pode ocupar uma área de 375 m².

Agora iremos calcular a área que o goleiro tem que defender e o atacante tem para acertar e fazer o gol. As medidas das traves são 7,32 m de largura e 2,44 m de altura, conhecendo essas medidas podemos calcular a área que o goleiro tem que defender.

Área = b x h, onde, b = comprimento e h = largura
A_{do gol} = 7,32 m x 2,44 m
A_{do gol} = 17,86 m²

A área entre as traves é de 17,86 m², ou seja, o goleiro tem que defender uma área mais de 17 metros quadrados.

Como estamos calculando várias áreas, podemos calcular também a área da grande área onde o goleiro pode trabalhar com a mão. A grande área tem 16,5 m de comprimento e 40,3 m de largura, com esses dados podemos calcular a área que o goleiro tem para trabalhar com as mãos.

A_{da grande área} = b x h, onde, b = comprimento e h = largura
A_{da grande área} = 16,5 m x 40,3m
A_{da grande área} = 664,95 m²

Figura 22: Futebol e a geometria

Agora iremos calcular a área do círculo central. O diâmetro do círculo central é de 18,30 m, atribuindo a ? ( pi ) o valor de 3,14 calcule a área do círculo central:

Área do círculo central = ? x r², onde, ? = pi = 3,14 e r = raio
Diâmetro = 18,30 m e ? = 3,14
r = Diâmetro / 2 ? r = 18,30 / 2 ? r = 9,15 m
A_{do círculo central} = 3,14 x ( 9,15 m )²
A_{do círculo central} = 3,14 x 83,72 m²
A_{do círculo central} = 262,88 m²

O círculo central possui então uma área de 262,88 m².
2.5.3 O Futebol e os desenhos táticos

Nas figuras 23, 24 e 25 podemos observar várias figuras geométricas em diferentes esquemas táticos adotados pelos principais times brasileiros, seleções e times estrangeiros.

No esquema 3-5-2 ( 3 zagueiros, 5 jogadores de meio de campo e 2 atacantes ), esquema adotado pelo técnico da seleção brasileira de futebol Luiz Felipe Scolari na disputa pelo pentacampeonato no mundial de 2002, disputado no JAPÃO e na CORÉIA DO SUL.

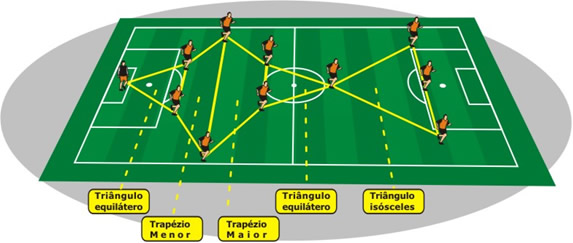
Conforme a figura 23, esse esquema mostra o desenho tático formado por diversas figuras geométricas como: triângulos equiláteros, triângulos isósceles e quadriláteros. É bom deixar claro que essas figuras podem variar de treinador para treinador, dependendo da característica dos jogadores e dos treinadores, mas independente da característica, todos os esquemas táticos poderá ser ilustrado através de figuras geométricas.

Figura 23: Esquema tático 3-5-2

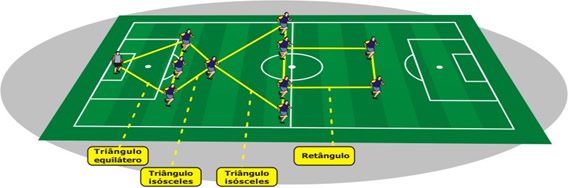
Já no esquema 4-4-2 ( 4 zagueiros, 4 jogadores de meio campo e 2 atacantes ), esquema adotado pelo técnico da seleção brasileira de futebol Carlos Alberto Parreira na disputa do tetracampeonato no mundial disputado nos Estados Unidos em 1994. Conforme a figura 24 abaixo esse esquema é formado por triângulo equilátero, trapézios, hexágono, quadrado e retângulo.

Figura 24: Esquema tático 4-4-2

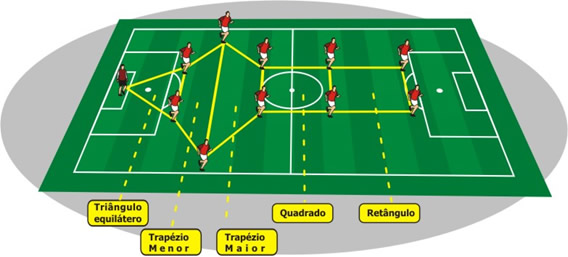
O esquema 4-3-3 ( 4 zagueiros, 3 jogadores de meio de campo e 3 atacantes), um esquema muito ofensivo que os treinadores usam quando estão em desvantagem no placar ou precisam reverter algum resultado desfavorável. Este esquema foi muito utilizado no passado, quando a prioridade era o ataque, o futebol bonito, chamado futebol arte. Este esquema pode ser observado várias figuras geométricas como: triângulos equiláteros, triângulos isósceles, trapézios, hexágonos, quadrados e retângulos.

Figura 25: Esquema tático 4-3-3

2.5.4 Esquemas táticos de algumas equipes de futebol

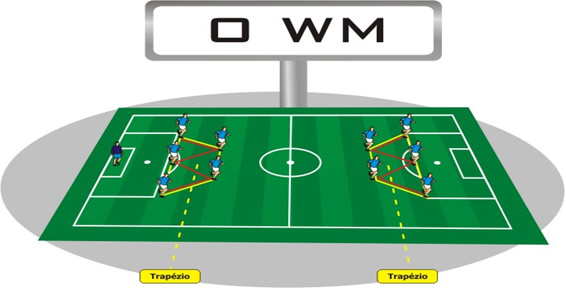
O esquema WM.

Figura 26: Esquema WM ou 3-2-5, Inglaterra da década de 20

O esquema WM formado por três zagueiros, dois jogadores de meio campo mais defensivo, dois jogadores de meio campo mais ofensivo e três atacantes, foi criado na década de 20 pelo inglês Chapman e foi trazido para o Brasil através do técnico Dori Kruescher. Neste esquema de jogo fica bem claro a formação de dois trapézios isósceles e em cada trapézio visualizamos três triângulos equiláteros.

2.5.4.2 Suíça de 1938.

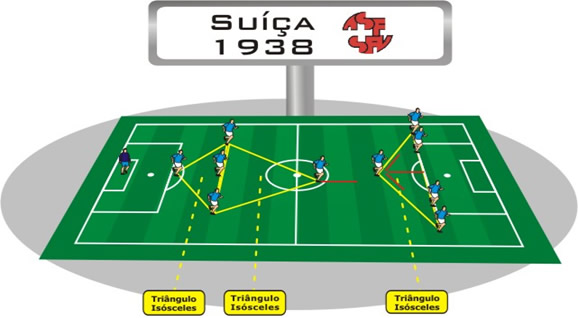
Figura 27: Esquema 4-1-5: Suíça de 1938

Também conhecido como Ferrolho Suíço, esquema com um zagueiro mais atrás, protegido por três zagueiros mais à frente, formando um triângulo isósceles, um jogador de meio campo mais recuado formando um triângulo equilátero e cinco atacantes formando também um triângulo isósceles. Foi um esquema inovador e surpreendente. E a base teórica deste esquema (marcação sobre pressão, meias/atacantes marcando os zagueiros fixo) é adotada até hoje.

O Vila Nova de 1951.

Figura 28: Esquema 4-2-4: Vila Nova de 1951

O 4-2-4 ( quatro zagueiros, dois jogadores de meio campo e quatro atacantes), foi criado com o intuito de diminuir a fragilidade defensiva do 2-3-5 e do WM. Neste esquema visualizamos um trapézio formado pelos jogadores da defesa e um paralelogramo formado pelos jogadores de ataque.

O Flamengo de 1954.

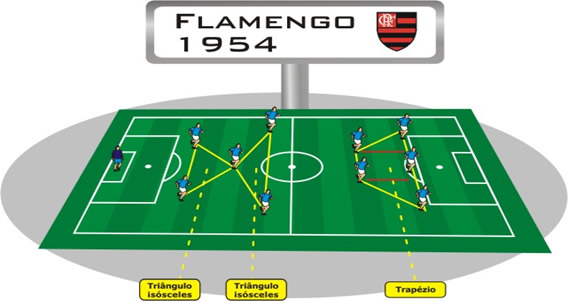
Figura 29: Esquema 2-3-5, Flamengo de 1954.

O primeiro esquema tático adotado no futebol moderno foi o 2-3-5. Não tinha muita preocupação ofensiva, jogavam com uma linha de 2 zagueiros, três homens de meio campo formando um triângulo equilátero, e cinco homens de ataque formando um trapézio.

A seleção brasileira de 1970.

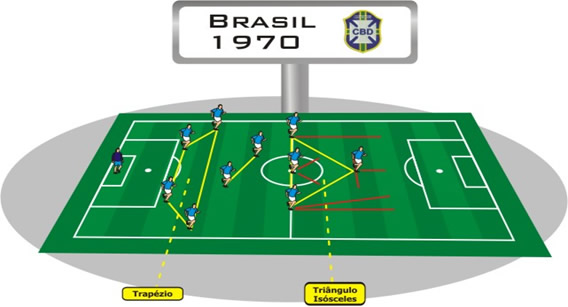
Figura 30: Esquema 4-2-4, Seleção Brasileira de 1970

Apesar do 4-2-4, o time jogava posicionado muito recuado para a época, sempre buscando o contra-ataque. Os quatro jogadores de defesa formavam um trapézio, dois jogadores de meio campo e quatro atacantes formando um triângulo isósceles. É considerada uma das melhores seleções de todos os tempos e tinha no comando do ataque Édson Arantes do Nascimento (Pelé), um dos maiores jogadores do mundo.

O Esquema com o Líbero.

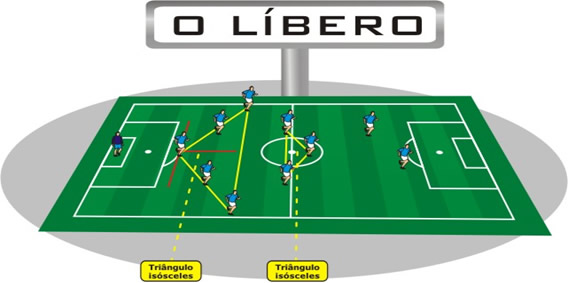
Figura 31: Esquema com o líbero

O líbero é responsável por proteger o gol, quando a defesa joga mais á frente, ele joga atrás do dois zagueiros. Neste esquema podemos observar um triângulo isósceles formado pelos jogadores de defesa e os alas, e no meio de campo outro triângulo isósceles.

O Barcelona de 1996.

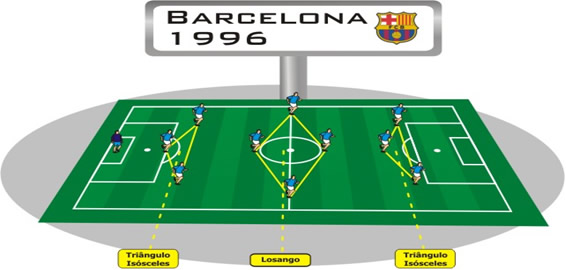
Figura 32: Barcelona de 1996

O Barcelona de 1996, jogava no 3-4-3 ( 3 zagueiros, 4 jogadores de meio campo e 3 atacantes ). Os times europeus, no início dos anos 90, geralmente adotavam um esquema que concentrasse bastante jogadores no meio campo, como o 3-4-3 e o 3-5-2. Esses esquemas possibilitam, teoricamente, maior proteção à defesa e maior apoio ao ataque. Além disso o líbero sempre foi usado. No esquema do Barcelona podemos observar um triângulo isósceles formado pelos jogadores da defesa, um losango formado pelos jogadores de meio campo e no ataque outro triângulo isósceles.

O Ajax de 1996.

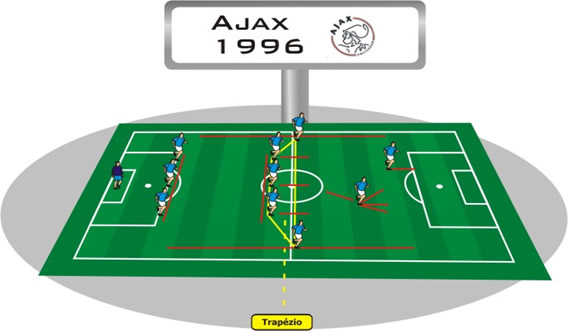
Figura 33: Ajax de 1996

O futebol mundial já parecia ter decretado o fim dos pontas ( jogadores que jogam abertos pelos lados do campo), já que era muito difícil achar jogadores tão versáteis para essa função. O Ajax reinventou esta formação e ganhou muitos títulos na década de 90. O Ajax jogava com uma linha (segmento de reta) com três zagueiros, três jogadores de meio campo e dois pontas abertos formando com isso um trapézio e dois atacantes se movimentando na frente.

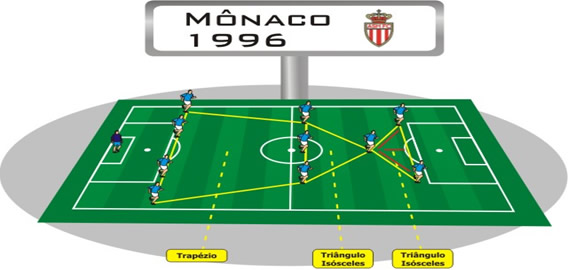
O Mônaco de 1996.

Figura 34: Mônaco de 1996

O Mônaco adotou um 4-4-2 ( quatro zagueiros, quatros jogadores de meio campo e dois atacantes ) um pouco diferente. Jogavam com uma linha de quatro zagueiros atrás, no meio campo tinha outra linha de três jogadores formando assim um trapézio e no ataque dois jogadores se movimentavam com a ajuda de um quarto homem de meio campo , formando dois triângulos isósceles.

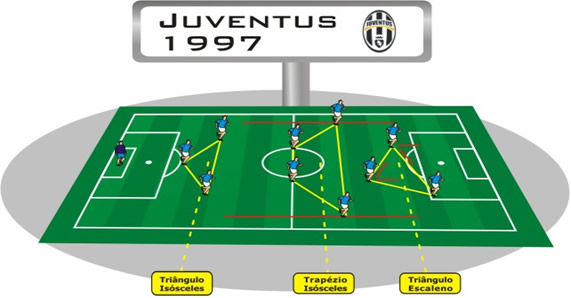
A Juventus de 1997.

Figura 35: Juventus de 1997

A equipe, quando atacada, defendia-se com os 3 zagueiros, formando um triângulo isósceles, juntamente com os dois laterais ou alas e os dois volantes formando um trapézio isósceles no meio campo. Já o ataque era formado por três jogadores formando assim um triângulo escaleno.

A Noruega de 1998.

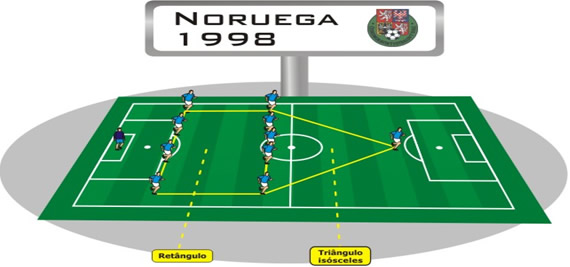
Figura 36: Noruega de 1998

O técnico Egil Olsen mostrou sua equipe num 4-5-1, com o meio campo e a defesa jogando em linha, com essa formação podemos observar um retângulo formado pela linha de quatro zagueiros e pela linha de cinco jogadores de meio campo. Já o ataque só tinha um jogador que formava um triângulo isósceles com o meio campo.

METODOLOGIA

O presente trabalho foi realizado através de pesquisa bibliográfica.

Tal pesquisa foi feita em sites, livros, periódicos, artigos científicos, na biblioteca do Centro Universitário de Lavras (UNILAVRAS), na biblioteca pública municipal da cidade de Perdões / MG e em acervo particular.

Foi feita uma análise criteriosa do material selecionado.

O período de realização do trabalho foi de fevereiro de 2007 a junho de 2008.

CONSIDERAÇÕES GERAIS

Para mudarmos a visão dos alunos sobre a Matemática, considerada por eles uma disciplina chata, difícil, desinteressante, é preciso torná-la prazerosa, útil e interessante.
Segundo o grande desafio que nós, educadores matemáticos, encontramos é tornar a Matemática interessante, isto é, atrativa, relevante, isto é útil e atual, isto é, integrada no mundo de hoje.

Já FAINGUELERNT(2004), diz que a Educação Matemática que queremos é aquela que se estenda muito além dos muros da escola do Ensino Fundamental, do Ensino Médio e do Ensino Superior.

Como podemos perceber ambos dizem que só conseguiremos alcançar o nosso objetivo de tornar a Matemática uma ciência gostosa e interessante quando torná-la aplicada, mostrando suas aplicações principalmente fora da escola, na vida real do aluno.

No caso específico da Geometria plana, por exemplo, esta enfrenta vários problemas que atrapalha o aprendizado do aluno. Segundo MANRIQUE (2004), alguns livros didáticos deixam a desejar pois os problemas geométricos propostos por estes, privilegiam resoluções algébricas, e poucos exigem raciocínio dedutivo ou demonstração. E ainda, quase não existe a passagem da Geometria empírica ( Geometria de experiências, observações ), para a Geometria dedutiva, além de poucos trabalhos focarem a leitura e a interpretação de textos matemáticos. Pavanello citado por Nascimento (2004), vai além, dizendo que outro fator importante é o tempo, ou seja, em algumas escolas o conteúdo geométrico é tratado apenas no final do livro didático e muitas vezes não dá tempo para ver o conteúdo, e quando sobra tempo, o mesmo não é visto completo e tem ficado relegado a um plano secundário.

Uma forma de se melhorar esta questão do tempo é intercalar as aulas de Geometria com as de Matemática, não deixando a Geometria para o final do ano. Como vimos existem vários fatores que atrapalham o aprendizado do aluno e contribuem para que ele se afaste cada vez mais da Geometria. Mas existem meios para revertemos esse quadro, principalmente mostrando a importância da Geometria e isso é possível com criatividade.

Lorenzato (1995) diz que a Geometria tem função essencial na formação dos indivíduos, pois possibilita uma interpretação mais completa do mundo, uma comunicação mais abrangente de idéias e uma visão mais equilibrada da Matemática. Já Hershkowitz citado por Fainguelernt (1999), diz que a Geometria é o ponto de encontro entre a Matemática como teoria e a Matemática como um recurso, ou seja, a Geometria é a ponte, a ligação do conteúdo teórico e o conteúdo prático.

Podemos considerar também que a Geometria está sempre presente em nossas vidas, é só olharmos nosso cotidiano, sempre tem uma figura geométrica, um ângulo, uma área, um volume para ser calculado, uma medida para ser transformada e um espaço para ser inovado. Isso é possível com a ajuda da Geometria.

Para tornar o ensino mais aplicado, mais acessível para o aluno, de forma que ele consiga usar a Matemática e a Geometria como uma ferramenta que irá ajudá-lo na sua caminhada, a linguagem desempenha um papel importante na constituição deste conhecimento. Freitas citado por Zuchi (2004), diz que ao mesmo tempo em que a linguagem é um fator importante para o desenvolvimento mental da criança, exercendo uma função organizadora e planejadora do seu pensamento, ela tem também uma função social e comunicativa.

Pois muitas vezes o professor falando uma linguagem muito científica não consegue passar a informação para o aluno, já o colega de classe, às vezes falando uma linguagem mais simples, consegue lhe transmitir o que o professor desejava.
Nosso objetivo é mostrar uma Geometria mais aplicada, mais prática, mostrando que se pode ensinar Geometria plana em parceria com um esporte que é paixão nacional, o futebol.

Segundo (FILLOS, 2006), a Geometria está em todos os lugares, principalmente nos campos e nas quadras de futebol. Já Morelli citado por Corrêa (2001), fala sobre a Geometria da bola e seu formato, formada por um icosaedro truncado. Silva ( 2004 ), fala sobre a Geometria aplicada no campo de futebol e algumas curiosidades interessantes, como área do campo de jogo, área do círculo central, as figuras geométricas encontradas no campo, e ainda mostra vários esquemas de times de todo o mundo e as figuras geométricas formadas por estes esquemas.

Como podemos observar os três autores falam dos conceitos matemáticos aplicados ao futebol e algumas curiosidades, que muitas vezes não notamos. Deste modo podemos tornar o ensino da Matemática, ou seja, da Geometria mais atraente, mais útil, mais interessante e instigante ao aluno. Aprendendo Geometria e ao mesmo tempo descobrindo os encantos de um esporte que é a paixão da maioria dos brasileiros.

www.somatica.com.br